TrafoStar - a unique tool for 3D BestFit Transformations
In a modern World with rising Automation in many Industries 3D Coordinates and their Coordinate Systems are the basis for many technical solutions.
Overdetermined 3D Transformations (also called 3D BestFit Transformation, 3D Helmert Transformation, 3D Coordinate Transformation, least squares Best Fit Transformation)
In many branches, areas and situations coordinates have to be transformed into different coordinate systems. This task can be performed by using simple mathematical methods. The conversion of the task is the determination of transformation parameters from coordinates of points that exist in two different coordinate systems (identical points). If more points exist than are necessary for the uniqueness of the calculation this overdetermination creates an equalization problem.
TrafoStar is an extremely flexible tool for determining transformation parameters and the residuals resulting from the equalization.
Applications for TrafoStar:
- Flexible 3D transformation of two 3D datasets with identical points
- Determination of the relation of robot coordinate system to vehicle coordinate system (e. g. for generating a RobCad file)
- Analysis of 3D coordinate measurements (accuracy, error parameters, gross error detection)
- Identification of error parameters of fixed coordinate measuring machines (CMM)
- Overdetermined determination of transformation parameters
- Subsequent transformation of new points with these transformation parameters
- Fitting of Coordinates to 3D rotationfigures like Paraboloids (nominal Data given as Shape Date)
TrafoStar receives two datasets as data input with the information: point number, x, y and z coordinate in form of ASCII-files. Alternatively an entry directly from the clipboard is possible. The calculation of the 3D transformation can be performed with outstanding flexibility:
- 1 to 13 parameter transformation
- affine 3D Coordinate Transformation
- 3 translations, 3 rotations, 3 scales, 3 affine parameters (angle x to y axis, angle z axis to xy plane and its azimuth) and one parameter (R-Dist) for possible non identicaly of indentical points
- Each parameter can be set independently to either fix or float, when set to fix a specific value for the parameter can be set by the user
Special Calculation options:
- The usage of each coordinate direction can be set using a table function, at the same time selected areas of the table can be edited at once
- alternative selection of robust L1 norm ([|v|]->min for gross error detection) and L2 norm ([vv]->min)
- Monte Carlo Simulation to analyze transformation parameters
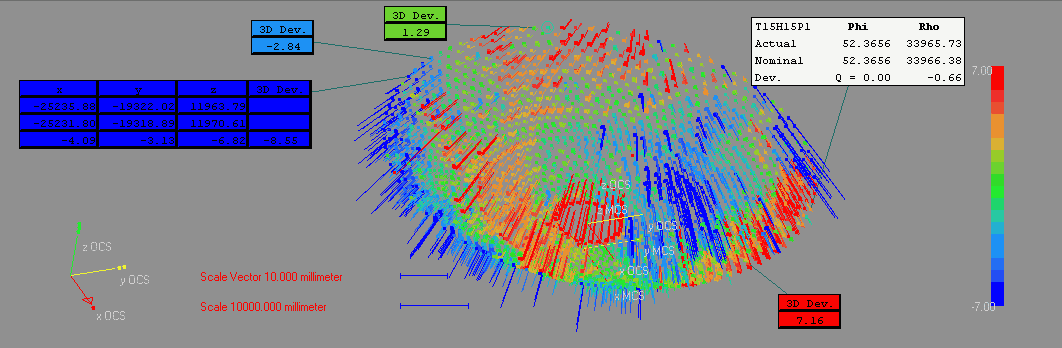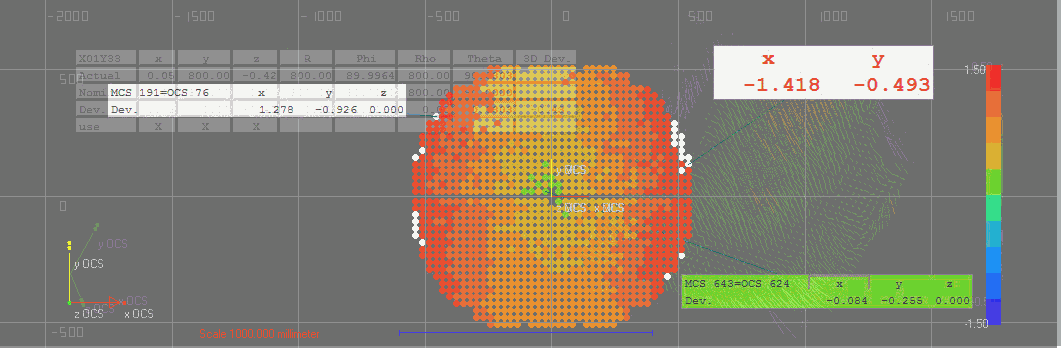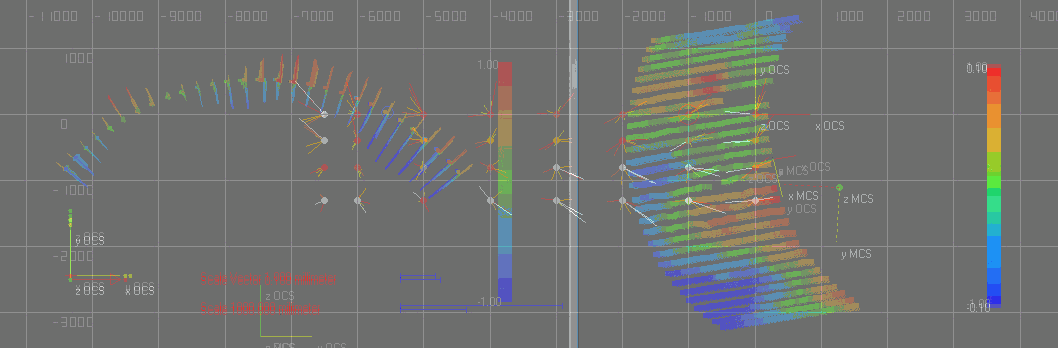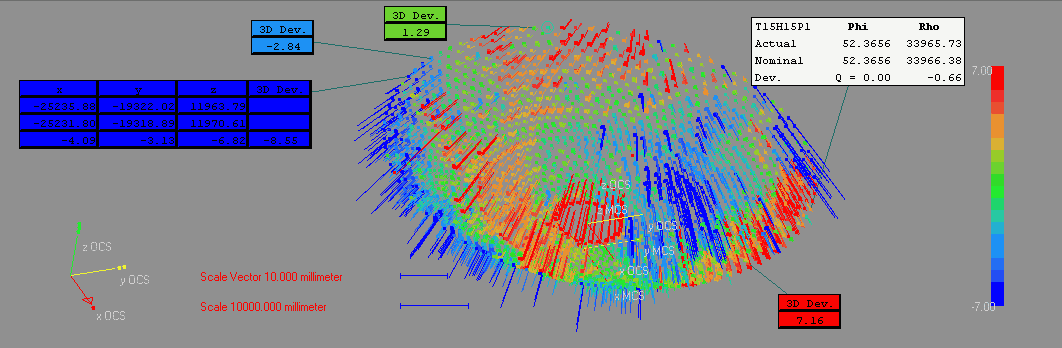
- graphic illustration of the points in the graphic-window, display of error vectors, change of magnitude, analysis mode for dynamic and magnified display of deviations
- Calculation of all possible combinations of rotation angles (Euler Angle, different rotation sequences, display of rotation matrix) as well as indication of both solutions possible for rotation angle